Who can Prove that 1 = -1?
I came across this really intriguing question a few day ago in my readings. You might find it somewhat geeky if math is not your thing; otherwise, let curiosity lead you.
In the very first lecture, a Mathematics PhD student, Alexander Farrugia’s class was greeted with the mathematical argument below by his lecturer. The argument states the 1 = -1. They had to spot what was wrong with it. The symbol means the square root.
So 1 = -1
I don’t think I will be giving away too much if I say the answer lies in the idea of the Real Numbers (Integers, Whole, Rational, etc…) and Complex / Imaginary Number System. Yep! you might have to call up on a bit of high school mathematics, but if the mathematical expression sends you into a nightmarish spin, just look up Complex or Imaginary Numbers on Google and you will see that they are just the “Parents” of Real Numbers. For some, this has a philosophical or even a spiritual component (Real coming from the Imaginary), but mathematically, there is nothing “Imaginary or Complex” about the Imaginary Numbers they are just as real as Reals are. Just ask anyone doing serious work in engineering, economics, statistics, etc..
Quick Aside:
Complex Numbers developed out of limitations of Real Numbers. By definition no Real Numbers exists, such that when you square it, the result is a negative number. In simplistic mathematical form it looks like this:
For any number x that is a member of the set of Real Numbers, then
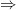
But what happens if you come across a situation in which you have a condition of this form.
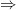
or written another way
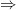
The answer, as your high school teacher so rightly told you, does not exists in the Real but Imaginary domain.
The lecturer then told Alex that the mistake lies in the rule : does not work for negative values of a and b. To see Alex’s full answer and explore a few other novel approaches to the question, check out the following source link below.
Source: Who Can Prove that 1 = -1?
Interesting Approach:
One particularly interesting, albeit less sophisticated approach from the post was:
Let 1 = -1 (statement 1 to be proven)
-1 = 1 (statement 2; follows directly from 1)
0 = 0
Since 2 wrongs cannot make a right, then the original statement cannot be right. Although this approach rests pretty much on semantics as opposed to rigorous mathematics, it was interesting none the less.
